자료구조의 중심을 나타내는 척도로 대표적인게 평균(average)과 중앙값(median)이 있습니다.
표본자료에 대하여 구한 평균을 표본평균(sample mean)이라하고, 모집단 전체 자료에 대한 평균을 모평균(population mean)이라고 한다.
표본평균은 모평균을 추정하는 값으로 좋은 성질을 가지고 있지만, 바깥점(outlier, 혹은 이상치)에 의하여 영향르 많이 받는다. 이러한 단저믈 보완하는 척도로 중앙값이 있으며, 중앙값은(median)은 자료들을 크기순으로 정렬(sort)하였을때 순서에 따라 가장 가우데 있는 값(middle value)를 의미한다. 자료의 갯수가 짝수개인경우 가운데 두값의 평균을 중앙값으로 사용한다.
표본중앙값은 표본평균과 달리 이상치에 영향을 받지 않은편으로 탐색적 자료분석에서 많이 사용된다. 반면 표본평균에 비하여 통계적 성질이 복잡하여 통계분석을 위한 이론 전개에 어려움이 많다는 단점을 자기고 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#2.5. 자료구조의 중심을 나타내는 척도 : 평균(mean), 중앙값(median)
x <- c(1,4,6,6,7,8,8,9,10,15)
#표본평균(sample mean)
mean(x)
[1] 7.4
#표본중앙값(sample median)
median(x)
[1] 7.5
y <- c(1,4,6,6,7,8,8,9,10,150)
#표본평균(sample mean)
mean(y)
[1] 20.9
#표본중앙값(sample median)
median(y)
[1] 7.5)],axis =1)
|
cs |
자료구조의 퍼짐을 나타내는 척도
표본평균을 중심 척도로 하여 나타낸 자료의 차이를 편차(deviation)라고 한다.
편차 = 자료값- 표본평균
편차들이 서로 상쇄되는것을 방지하기 위하여 표본표준편차(sample standard deviation)또는 표본분산(sample variance)가 있다. 모집단 전체자료의 분산인 모분산(popuation variance)이라고 한다.
|
1
2
3
4
5
6
7
8
|
#예제2.9 표본분산과 표본표준편차를 구하라
x <- c(1,3,4,6,6,7,8,8,9,10,15)
#표본분산(sample variance)
var(x)
[1] 14.2
#표본표준편차(sample standard deviation)
sd(x)
[1] 3.768289
|
cs |
표본분산은 자료가 많은 경우 계산량이 많으므로 퍼짐의 정도를 손쉽게 산출할수 있는 척도로서 표본범위(sample range)가 있다.
표본범위 = 자료의 최대값 - 자료의 최소값
표본범위의 단점을 보완하는 척도로 사분위수를 이용한 표본사분위수 범위(sample interquartile range)가 있다.
표본사분위수범위(IQR) = 제3사분위수 - 제1사분위수
|
1
2
3
4
5
6
|
#표본사분위수범위(sample interquartile range)
x <- c(1,3,4,6,6,7,8,8,9,10,15)
#사분위수
quantile(x,c(0.25,0.75))
25% 75%
5.0 8.5
|
cs |
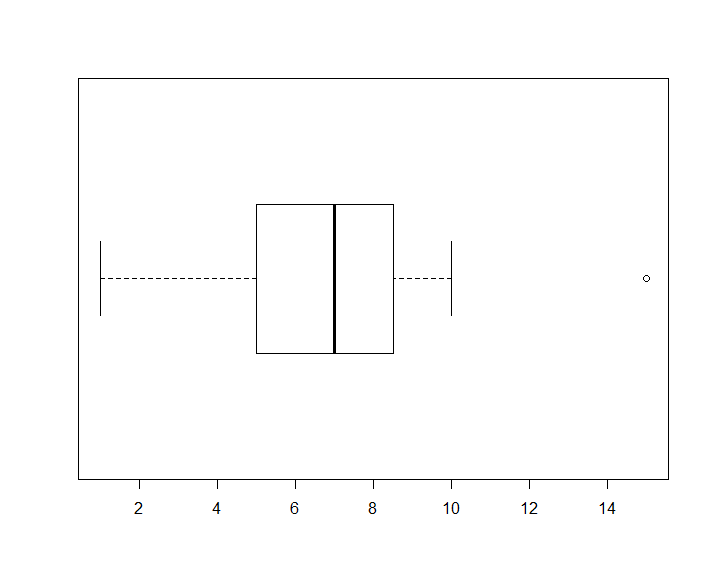
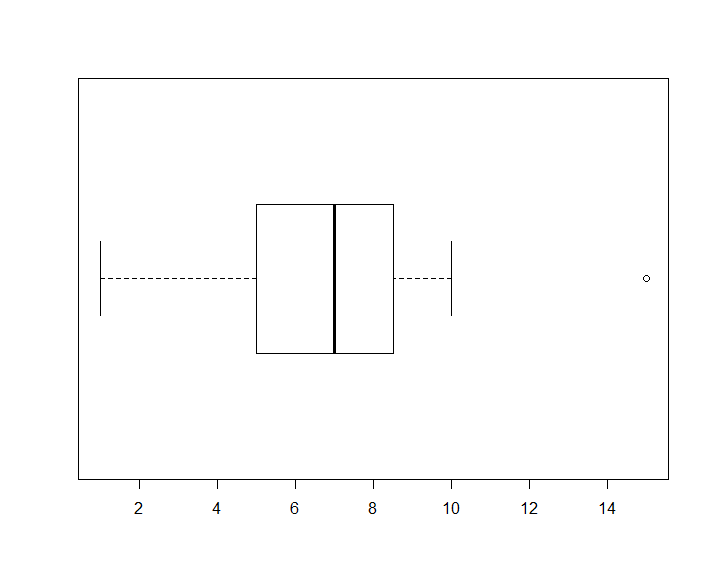
사분위수들과 최솟값, 최대값으로 이루어진 그림으로 상자와 수염그림(box-and-whisker plot)이 있다.
상자와수염그림(boxplot)을 구성하는 5개의 값을 다섯숫자요약(5-number summary)라고 하며
최솟값, 제1사분위수, 중앙값(제2사분위수),제3사분위수, 최댓값 이 포함된다.
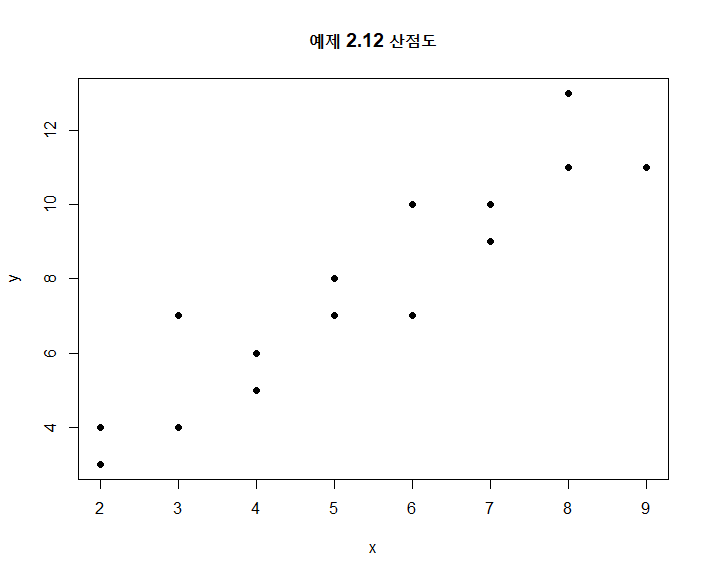
이변량 양적자료의 표현은 이차원 평면상에 흩뿌려진 점으로 나타내 그림을 산점도(scatter diagram)이라고 한다.
|
1
2
3
4
5
|
#2.9 이변량 양적 자료의 표현
x<- c (2,3,4,5,6,7,8,9,4,6,3,7,2,5,8)
y<- c (4,7,6,8,10,9,13,11,5,7,4,10,3,7,11)
#산점도
plot(x,y,pch=19 , main="예제 2.12 산점도")
|
cs |
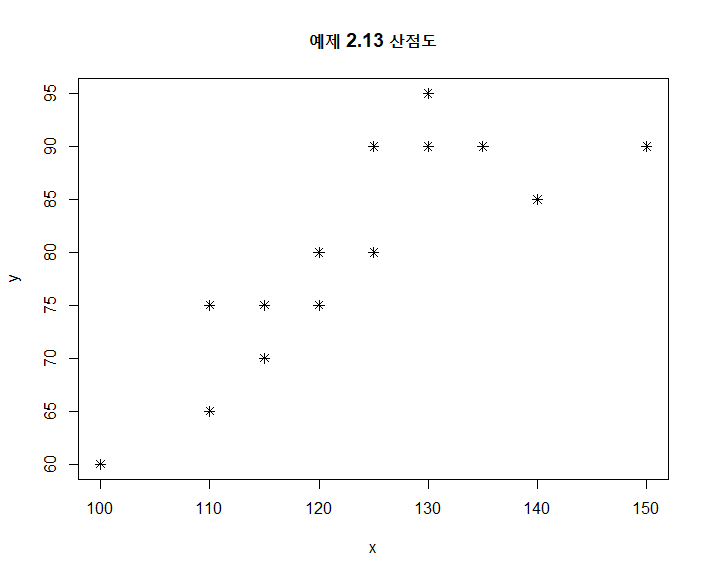
선형관계의 척도로 가장 많이 사용되는 것이 상관계수(correlation coefficient)이다.
|
1
2
3
4
5
6
7
|
#2.9.2 선형관계의 척도로서의 상관계수 : cor()
x <- c(110,130,125,120,115,120,125,130,150,140,100,110,115,120,135)
y <- c(75,90,80,80,70,75,90,95,90,85,60,65,75,75,90)
plot(x,y,pch=8,main="예제 2.13 산점도")
#상관계수
cor(x,y)
[1] 0.8384023
|
cs |
'아재도 하는 통계' 카테고리의 다른 글
| [50원] [통계학개론] 제2장 자료의 구조(1) (0) | 2019.08.20 |
|---|